Vortex Rossby Wave Theory and Literature

        The term ‘vortex Rossby wave’ (VRW) and a formal theory for the propagation and interaction of the waves with the mean flow was first presented by Montgomery and Kallenbach (1997) and later generalized by McWilliams et al. (2003).  They showed that the axisymmetrization of potential vorticity (PV) anomalies, such as those generated through moist-convective processes, by the strong horizontal shear of the mean vortex was accompanied by outward propagating VRWs that accelerated the tangential winds near the radius of wave excitation.  The VRWs propagated on the radial gradient of mean storm vorticity, analogous to Rossby waves in the large-scale circulation (MacDonald 1968).  Montgomery and Enagonio (1998) and Möller and Montgomery (1999, 2000) used a three-dimensional quasigeostrophic model and a fully non-linear asymmetric balance model, respectively, to show tropical cyclogenesis and intensification could occur through the axisymmetrization and ingestion of like-signed PV anomalies by a parent vortex with a monopole vorticity structure.  Furthermore, through the continual injection of PV pulses (to simulate the effects of continuos convection), Möller and Montgomery (2000) showed that an initially tropical storm-strength vortex could develop a warm core and attain hurricane strength on realistic time scales.
  
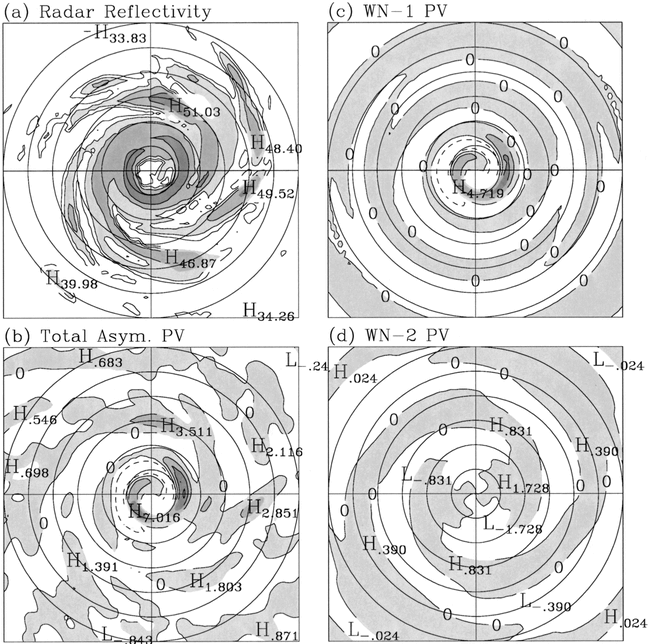
        Tropical cyclones exhibiting monopoles of vorticity are, however, likely to occur only during the tropical storm and weak hurricane stages of development, while rapidly intensifying or mature hurricanes with well-developed eyewalls usually exhibit rings of elevated PV on the inner edge of the eyewall (Kossin and Eastin 2001; Mallen et al. 2005).  Wang (2001, 2002a,b) showed that the asymmetric structure within 70 km of the center of his modeled vortex with an annular tower of PV was dominated by wavenumber 1 and 2 VRWs.  Similar results were found by Chen et al. (2003), who showed that the leading modes in wave activity in the core were VRWs, generated in the lower eyewall through diabatic heating.  The waves were found to be well coupled to convection as the enhanced vertical velocity associated with the wave led to the appearance of inner spiral rainbands (Chen and Yau 2001; Wang 2002b).
 
Figure 12 of Wang (2002b) (left) and Figure 10 of Wang (2002a) (right): (Left) a) Radar reflectivity, b) total asymmetric PV and its c) wavenumber 1 and d) wavenumber 2 components with positive values shaded, at 850 hPa after 84 h 30 min of simulation, showing the relationship between inner and outer rainbands and the activity of VRWs.  (Right) The wavenumber 1 component of a) PV and b)-h) PV tendencies due to terms on the right hand side of the perturbation PV equation and the total local PV tendency (i) estimated from all terms at 86 h 30 min of simulation at 850 hPa.  b) Horizontal and vertical advection of perturbation PV by the symmetric cyclone flow (LADV); c) horizontal and vertical advection of symmetric PV by the asymmetric flow (BETA); d) PV flux divergence due to asymmetric diabatic heating (DIABE); e) PV flux divergence due to symmetric diabatic heating (DIABM); f) non-conservative PV flux divergence due to symmetric friction (FRICM); g) PV flux divergence due to asymmetric friction (FRICE); h) PV tendency due to all non-linear eddy processes (NONL).  The domain shown in each panel is 120 km x 120 km and circles are every 30 km from the center.  Contour interval is 1 PVU in a) and 1 PVU day-1 in the rest with positive (anticyclonic) PV or PV tendency shaded.

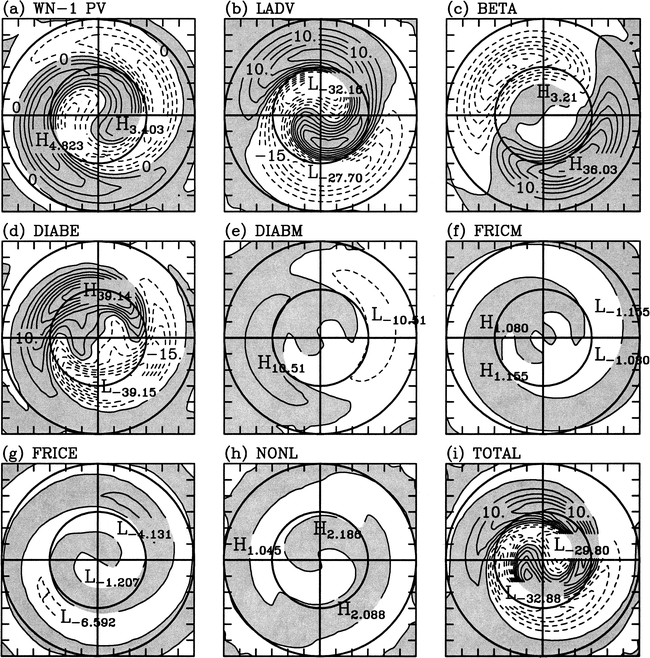
        Unlike their monopole vortex counterparts discussed previously, numerical simulations of vortices with annular PV rings have failed to document a consistent influence of VRWs on the intensity of the mean vortex.  Chen and Yau (2001), Möller and Shapiro (2002), and Chen et al. (2003) documented maximum VRW activity near the radius of maximum wind (RMW), and the transport of high angular momentum and PV by the VRWs radially inward, from the eyewall towards the eye.  This inward transport of high vorticity by VRWs was associated with intensification, as the maximum tangential wind spin-up occurred just inside the RMW, causing the RMW to propagate inward with time and leading to contraction of the eyewall.  On the other hand, Wang (2002b) and Chen and Yau (2003) found VRW-mean flow interactions tended to inhibit strengthening as the VRWs acted to spin up the tangential winds directly in the eye and decelerate the winds at the RMW.




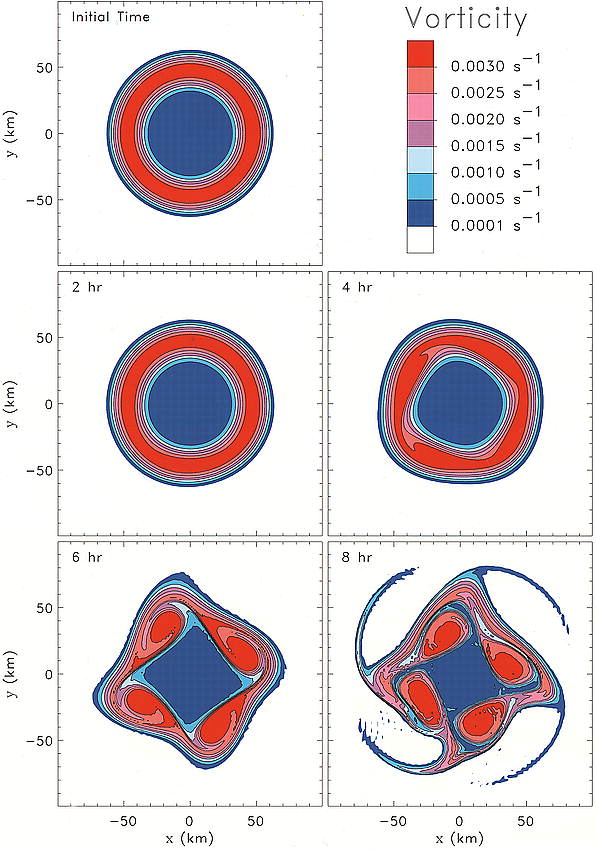
Further complicating the dynamics in storms with elevated rings of vorticity in the eyewall is the possibility of barotropic instability.  Schubert et al. (1999) showed that an annular vorticity structure contains counterpropagating VRWs with respect to the flow on its inner and outer vorticity gradients.  If these waves became phase-locked, they grew in concert and led to the exponential instability of the ring, whereby the eyewall vorticity pooled into discrete areas, creating mesovortices.  Depending on the initial conditions of the PV ring, the mesovortices either merged over time and relaxed to a monopole (Schubert et al. 1999; Chen and Yau 2003), or remained separate to form a quasi-steady rotating lattice of vortices that gave the appearance of elliptical (two mesovortices) or polygonal (four or more mesovortices) eyewalls (Kossin and Schubert 2001).  In either case, the asymmetric mixing by the mesovortices between the eye and eyewall brought high eyewall vorticity into the eye and low vorticity from the eye outward.  In order to conserve angular momentum during such a rearrangement, some high eyewall vorticity was also mixed outward, taking the form of vorticity filaments, or spiral bands with VRW characteristics (Kuo et al. 1999; Schubert et al. 1999).
       

Left, Figure 3a of Schubert et al. (1999): Vorticity contour plots for the representative experiment.  The model domain is 600 km x 600 km, but only the inner 200 km x 200 km is shown.  The contours begin at 0.0005 s-1.  Low vorticity values are shaded blue and high vorticity values are shaded red.  Vorticity from 0 h to 8 h is shown.
       








 
       

        Given the copious amount of numerical modeling studies dealing with VRWs in recent years, it is somewhat surprising that only a handful of observational studies have examined convective asymmetries in the core of tropical cyclones and evaluated whether they exhibit the properties of the VRWs seen in numerical models.  Muramatsu (1986) documented 15 h of counterclockwise rotating eyewall shapes in Typhoon Wynne (1980).  He made a fascinating analogy between polygonal eyewalls and the multiple vortices sometimes seen rotating around the inside of a parent tornado vortex, and noted barotropic instability as a possible cause of both phenomena.  Kuo et al. (1999) and Reasor et al. (2000) documented elliptical eyewalls in Typhoon Herb (1996) and Hurricane Olivia (1994), respectively.  Both studies noted elliptical eyewalls that rotated at approximately half the maximum tangential wind speed (Vmax) with deep convection located at the ends of the major axis of the ellipse. 

        Other observational studies have confirmed the barotropic modeling results of Schubert et al. (1999) and Kossin and Schubert (2001) by documenting the existence of multiple mesovortices in the eye and substantial mixing between the eye and eyewall.  Kossin et al. (2002, 2004) and Kossin and Schubert (2004) showed spectacular photographic and satellite imagery of low-level vortical swirls in the eyes of multiple Atlantic and Pacific basin tropical cyclones that closely resembled the long-lived mesovortices of Kossin and Schubert (2001).  Using flight-level reconnaissance data, Kossin and Eastin (2001) showed that the radial profiles of vorticity and equivalent potential temperature can undergo a rapid transition from a barotropically unstable regime with maximum values of vorticity and equivalent potential temperature in the eyewall, to a stable regime with both maxima in the eye.  Knaff et al. (2003) found that the development of annular hurricanes was systematically preceded by a dramatic asymmetric mixing event between the eye and the eyewall involving one or more mesovortices.


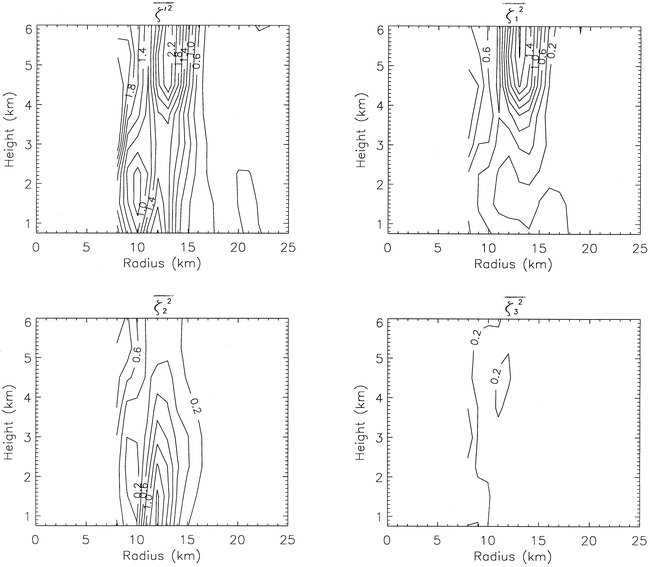
The most complete observational investigation of asymmetric vorticity dynamics and VRWs in the core of a tropical cyclone was carried out by Reasor et al. (2000) in Hurricane Olivia (1994).  The vorticity asymmetry in the core was dominated by azimuthal wavenumber 2 below 3 km, and wavenumber 1 above 3 km, with maximum values of both found near the RMW.  The wavenumber 1 signature was hypothesized to be the result of environmental vertical wind shear, as an increase in the magnitude of the wavenumber 1 asymmetry coincided with an increase in the magnitude of the vertical shear.  The wavenumber 2 asymmetry was found to be the most unstable wavenumber and the natural by-product of the breakdown of the unstable vorticity ring that Olivia (1994) possessed at the beginning of the period of study.  Reasor et al. (2000) also observed trailing bands of vorticity, 5-10 km wide, associated with high reflectivity, outside the eyewall of Olivia (1994).  They hypothesized that these bands were symmetrizing VRWs resulting from the expulsion of high vorticity air from the core during mixing.

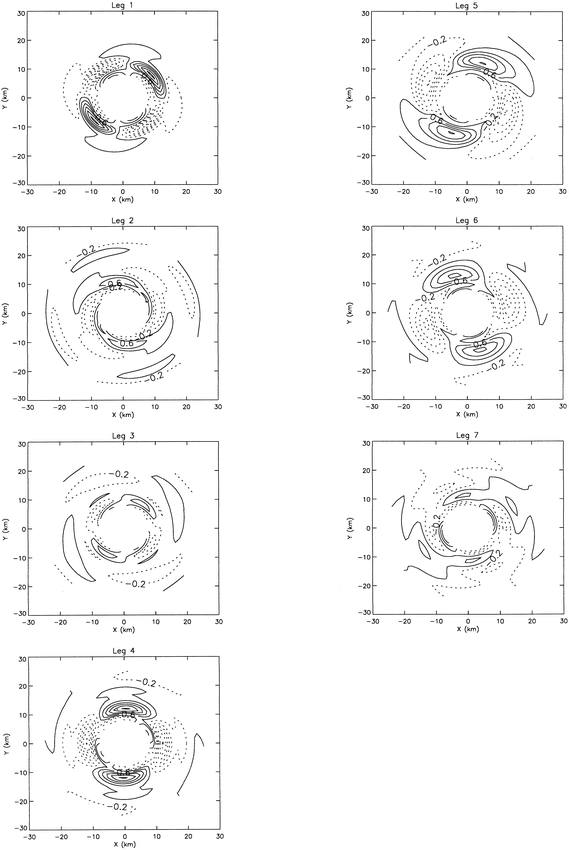
Left, Figure 12 of Reasor et al. (2000): Radius-height structure of the azimuthal variance of vorticity averaged over the period 2027-2355 UTC.  Also shown are the individual wavenumber contributions (1-3) to the azimuthal variance (i.e., wavenumber components of vorticity squared and azimuthally averaged).  Contour interval is 0.2x10-6 s-2.





             
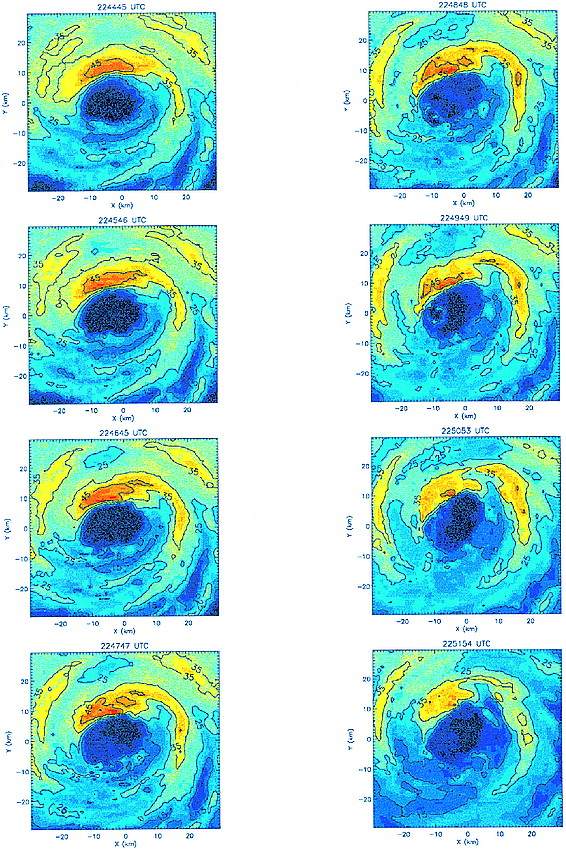
Above, Figures 15 (right) and 16 (left) of Reasor et al. (2000): (Left) Hurricane Olivia inner core lower fuselage reflectivity composites at 3 km height.  Period spanned is 2244-2251 UTC at 1 minute intervals.  The contour interval is 10 dBZ.  (Right) Azimuthal wavenumber 2 component of vorticity vertically averaged over the lowest 3 km for each flight.  Contour interval is 0.4x10-3 s-1.  Negative values are depicted by the dashed curves.

References:
Chen, Y., and M. K. Yau, 2001: Spiral bands in a simulated hurricane. Part I: Vortex Rossby wave verification. J. Atmos. Sci., 58, 2128-2145.

Chen, Y., G. Brunet, and M. K. Yau, 2003: Spiral bands in a simulated hurricane. Part II: Wave activity diagnostics. J. Atmos. Sci., 60, 1239-1256.

Chen, Y., and M. K. Yau, 2003: Asymmetric structures in a simulated landfalling hurricane. J. Atmos. Sci., 60, 2294-2312.

Corbosiero, K. L., J. Molinari, A. R. Aiyyer and M. L. Black, 2006: The structure and evolution of Hurricane Elena (1985). Part II: Convective asymmetries and evidence for vortex Rossby waves. Mon. Wea. Rev., 134, 3073-3091.

Knaff, J. A., J. P. Kossin, and M. DeMaria, 2003: Annular hurricanes. Wea. Forecasting, 18, 204-223.

Kossin, J. P., and M. D. Eastin, 2001: Two distinct regimes in the kinematic and thermodynamic structure of the hurricane eye and eyewall. J. Atmos. Sci., 58, 1079-1090.

Kossin, J. P., and W. H. Schubert, 2001: Mesovortices, polygonal flow patterns, and rapid pressure falls in hurricane-like vortices. J. Atmos. Sci., 58, 2196-2209.

Kossin, J. P., B. D. McNoldy, and W. H. Schubert, 2002: Vortical swirls in hurricane eye clouds. Mon. Wea. Rev., 130, 3144-3149.

Kossin, J. P., and W. H. Schubert, 2004: Mesovortices in Hurricane Isabel. Bull. Amer. Meteor. Soc., 85, 151-153.

Kossin, J. P., W. H. Schubert, C. Velden, M. Black, P. Black, R. Zehr, S. Aberson, and J. Dunion, 2004: Mesovortices in Hurricane Isabel (2003).  Preprints, 26th Conf. on Hurricanes and Tropical Meteorology, Miami, FL, Amer. Met. Soc., 447-448.

Kuo, H.-C., R. T. Williams, and J.-H. Chen, 1999: A possible mechanism for the eye rotation of Typhoon Herb. J. Atmos. Sci., 56, 1659-1673.

MacDonald, N. J., 1968: The evidence for the existence of Rossby-type waves in the hurricane vortex. Tellus, 20, 138-150.

Mallen, K. J., M. T. Montgomery, and B. Wang, 2005: Re-examining the near-core radial structure of the tropical cyclone primary circulation: Implications for vortex resiliency. J. Atmos. Sci., 62, 408-425.

McWilliams, J. C., L. P. Graves, and M. T. Montgomery, 2003: A formal theory for vortex Rossby waves and vortex evolution. Geophys. Astrophys. Fluid Dynamics, 97, 275-309.

Möller, J. D., and M. T. Montgomery, 1999: Vortex Rossby waves and hurricane intensification in a barotropic model. J. Atmos. Sci., 56, 1674-1687.

Möller, J. D., and M. T. Montgomery, 2000: Tropical cyclone evolution via potential vorticity anomalies in a three-dimensional balance model. J. Atmos. Sci., 57, 3366-3387.

Möller, J. D., and L. J. Shapiro, 2002: Balanced contributions to the intensification of Hurricane Opal as diagnosed from a GFDL model forecast. Mon. Wea. Rev., 130, 1866-1881.

Montgomery, M. T., and R. J. Kallenbach, 1997: A theory for vortex Rossby waves and its application to spiral bands and intensity changes in hurricanes. Quart. J. Roy. Meteor. Soc., 123, 435-465.

Montgomery, M. T., and J. Enagonio, 1998: Tropical cyclogenesis via convectively forced vortex Rossby waves in a three-dimensional quasigeostrophic model. J. Atmos. Sci., 55, 3176-3207.Montgomery, M. T., H. D. Snell, and Z. Yang, 2001: Axisymmetric spindown dynamics of hurricane-like vortices. J. Atmos. Sci., 58, 421-435.

Muramatsu, T., 1986: The structure of polygonal eye of a typhoon. J. Meteor. Soc. Japan, 64, 913-921.

Reasor, P. D., M. T. Montgomery, F. D. Marks, Jr. and J. F. Gamache, 2000: Low-wave number structure and evolution of the hurricane inner core observed by airborne dual-Doppler radar. Mon. Wea. Rev., 128, 1653-1680.

Schubert, W. H., M. T. Montgomery, R. K. Taft, T. A. Guinn, S. R. Fulton, J. P. Kossin, and J. P. Edwards, 1999: Polygonal eyewalls, asymmetric eye contraction, and potential vorticity mixing in hurricanes. J. Atmos. Sci., 56, 1197-1223.

Wang, Y., 2001: An explicit simulation of tropical cyclones with a triply nested movable mesh primitive equation model: TCM3. Part I: Model description and control experiment. Mon. Wea. Rev., 129, 1370-1394. 

Wang, Y., 2002a: Vortex Rossby waves in a numerically simulated tropical cyclone. Part I: Overall structure, potential vorticity, and kinetic energy budgets. J. Atmos. Sci., 59, 1213-1238.

Wang, Y., 2002b: Vortex Rossby waves in a numerically simulated tropical cyclone. Part II: The role in tropical cyclone structure and intensity changes. J. Atmos. Sci., 59, 1239-1262.