01_GriddedDiagnostics_TempAdvection_ERA5

01_GriddedDiagnostics_TempAdvection_ERA5#

In this notebook, we’ll cover the following:#

Select a date and access the ERA5 dataset
Subset the desired variables along their dimensions
Calculate and visualize diagnostic quantities.
Smooth the diagnostic field.

0) Imports #

import xarray as xr
import pandas as pd
import numpy as np
from datetime import datetime as dt
from metpy.units import units
import metpy.calc as mpcalc
import cartopy.crs as ccrs
import cartopy.feature as cfeature
import matplotlib.pyplot as plt

1) Specify a starting and ending date/time, regional extent, vertical levels, and access the ERA5#

Restrict your date range to no more than 7 days!

# Areal extent
lonW = -100
lonE = -60
latS = 25
latN = 55
cLat, cLon = (latS + latN)/2, (lonW + lonE)/2

# Recall that in ERA5, longitudes run between 0 and 360, not -180 and 180
if (lonW < 0 ):
    lonW = lonW + 360
if (lonE < 0 ):
    lonE = lonE + 360
    
expand = 1
latRange = np.arange(latS - expand,latN + expand,.25) # expand the data range a bit beyond the plot range
lonRange = np.arange((lonW - expand),(lonE + expand),.25) # Need to match longitude values to those of the coordinate variable

# Vertical level specification
pLevel = 850
levStr = f'{pLevel}'

startYear = 2007
startMonth = 2
startDay = 14
startHour = 12
startMinute = 0
startDateTime = dt(startYear,startMonth,startDay, startHour, startMinute)

endYear = 2007
endMonth = 2
endDay = 14
endHour = 12
endMinute = 0
endDateTime = dt(endYear,endMonth,endDay, endHour, endMinute)

delta_time = endDateTime - startDateTime
time_range_max = 7*86400

if (delta_time.total_seconds() > time_range_max):
        raise RuntimeError("Your time range must not exceed 7 days. Go back and try again.")

The variable names and two of the dimension names in our local 2023-2024 archive differ from those in the Google Cloud Platform-hosted multi-decade archive. In the cell below, we employ a dictionary that translates the former to the latter. We then pass the dictionary to Xarray's rename_dims and rename_vars functions to perform the renamings.

Chunks: See this link for more info about chunking in Xarray.

Wb2EndDate = dt(2023,1,10)
if (endDateTime <= Wb2EndDate):
    ds = xr.open_dataset(
     'gs://weatherbench2/datasets/era5/1959-2023_01_10-wb13-6h-1440x721.zarr', 
     chunks={'time': 48},
     consolidated=True,
     engine='zarr'
)
else: 
    import glob, os
    input_directory = '/free/ktyle/era5'
    files = glob.glob(os.path.join(input_directory,'*.nc'))
    varDict = {'valid_time': 'time', 
               'pressure_level': 'level',
               'msl': 'mean_sea_level_pressure',
               'q': 'specific_humidity',
               't': 'temperature',
               'u': 'u_component_of_wind',
               'v': 'v_component_of_wind',
               'w': 'vertical_velocity',
               'z': 'geopotential'}
    dimDict = {'valid_time': 'time',
               'pressure_level': 'level'}
    ds = xr.open_mfdataset(files).rename_dims(dimDict).rename_vars(varDict)

Examine the Dataset

ds

<xarray.Dataset> Size: 47TB
Dimensions:                                           (time: 93544,
                                                       latitude: 721,
                                                       longitude: 1440,
                                                       level: 13)
Coordinates:
  * latitude                                          (latitude) float32 3kB ...
  * level                                             (level) int64 104B 50 ....
  * longitude                                         (longitude) float32 6kB ...
  * time                                              (time) datetime64[ns] 748kB ...
Data variables: (12/50)
    10m_u_component_of_wind                           (time, latitude, longitude) float32 388GB dask.array<chunksize=(48, 721, 1440), meta=np.ndarray>
    10m_v_component_of_wind                           (time, latitude, longitude) float32 388GB dask.array<chunksize=(48, 721, 1440), meta=np.ndarray>
    2m_dewpoint_temperature                           (time, latitude, longitude) float32 388GB dask.array<chunksize=(48, 721, 1440), meta=np.ndarray>
    2m_temperature                                    (time, latitude, longitude) float32 388GB dask.array<chunksize=(48, 721, 1440), meta=np.ndarray>
    angle_of_sub_gridscale_orography                  (latitude, longitude) float32 4MB dask.array<chunksize=(721, 1440), meta=np.ndarray>
    anisotropy_of_sub_gridscale_orography             (latitude, longitude) float32 4MB dask.array<chunksize=(721, 1440), meta=np.ndarray>
    ...                                                ...
    v_component_of_wind                               (time, level, latitude, longitude) float32 5TB dask.array<chunksize=(48, 13, 721, 1440), meta=np.ndarray>
    vertical_velocity                                 (time, level, latitude, longitude) float32 5TB dask.array<chunksize=(48, 13, 721, 1440), meta=np.ndarray>
    volumetric_soil_water_layer_1                     (time, latitude, longitude) float32 388GB dask.array<chunksize=(48, 721, 1440), meta=np.ndarray>
    volumetric_soil_water_layer_2                     (time, latitude, longitude) float32 388GB dask.array<chunksize=(48, 721, 1440), meta=np.ndarray>
    volumetric_soil_water_layer_3                     (time, latitude, longitude) float32 388GB dask.array<chunksize=(48, 721, 1440), meta=np.ndarray>
    volumetric_soil_water_layer_4                     (time, latitude, longitude) float32 388GB dask.array<chunksize=(48, 721, 1440), meta=np.ndarray>

3) Calculate and visualize diagnostic quantities.#

Define our subsetted coordinate arrays of lat and lon. Pull them from any of the DataArrays. We’ll need to pass these into the contouring functions later on.

lats = T.latitude
lons = T.longitude

First, let’s just plot contour lines of temperature and wind barbs.#

Unit conversions#

We will create new objects for T, U and V in knots, since we will want to preserve the original units (m/s) when it comes time to calculate temperature advection.

TCel = T.metpy.convert_units('degC')
UKts = U.metpy.convert_units('kts')
VKts = V.metpy.convert_units('kts')

Create an array of values for the temperature contours: since we are using contour lines, simply define a range large enough to encompass the expected values, and set a contour interval.

TCel.min().values, TCel.max().values

(array(-25.867737, dtype=float32), array(17.190002, dtype=float32))

cint = 2
minT, maxT = (-30,22)
TContours = np.arange(minT, maxT, cint)

Make the map#

constrainLat, constrainLon = (0.5, 4.0)
proj_map = ccrs.LambertConformal(central_longitude=cLon, central_latitude=cLat)
proj_data = ccrs.PlateCarree() # Our data is lat-lon; thus its native projection is Plate Carree.
res = '50m'

Although there is just a single time in our time range, we’ll still employ a loop here in case we wanted to include multiple times later on.

for time in dateList:
    print(f"Processing {time}")
    
    # Create the time strings, for the figure title as well as for the file name.
    timeStr = dt.strftime(time,format="%Y-%m-%d %H%M UTC")
    timeStrFile = dt.strftime(time,format="%Y%m%d%H")

    tl1 = f'ERA5, Valid at: {timeStr}'
    tl2 = f'{levStr} hPa temperature (°C) and wind (kts)'
    
    title_line = f'{tl1}\n{tl2}\n'
    
    fig = plt.figure(figsize=(21,15)) # Increase size to adjust for the constrained lats/lons
    ax = fig.add_subplot(1,1,1,projection=proj_map)
    ax.set_extent ([lonW+constrainLon,lonE-constrainLon,latS+constrainLat,latN-constrainLat])
    ax.add_feature(cfeature.COASTLINE.with_scale(res))
    ax.add_feature(cfeature.STATES.with_scale(res),edgecolor='brown')
    
    # Need to use Xarray's sel method here to specify the current time for any DataArray you are plotting.
    
    # 1. Contour lines of temperature
    cT = ax.contour(lons, lats, TCel.sel(time=time), levels=TContours, colors='orange', linewidths=3, transform=proj_data)
    ax.clabel(cT, inline=1, fontsize=12, fmt='%.0f')
    
    # 4. wind barbs
    # Plotting wind barbs uses the ax.barbs method. Here, you can't pass in the DataArray directly; you can only pass in the array's values.
    # Also need to sample (skip) a selected # of points to keep the plot readable.
    # Remember to use Xarray's sel method here as well to specify the current time.
    skip = 5
    ax.barbs(lons[::skip],lats[::skip],UKts.sel(time=time)[::skip,::skip].values, VKts.sel(time=time)[::skip,::skip].values, color='purple',zorder=2,transform=proj_data)

    title = plt.title(title_line,fontsize=16)
    

Processing 2007-02-14 12:00:00

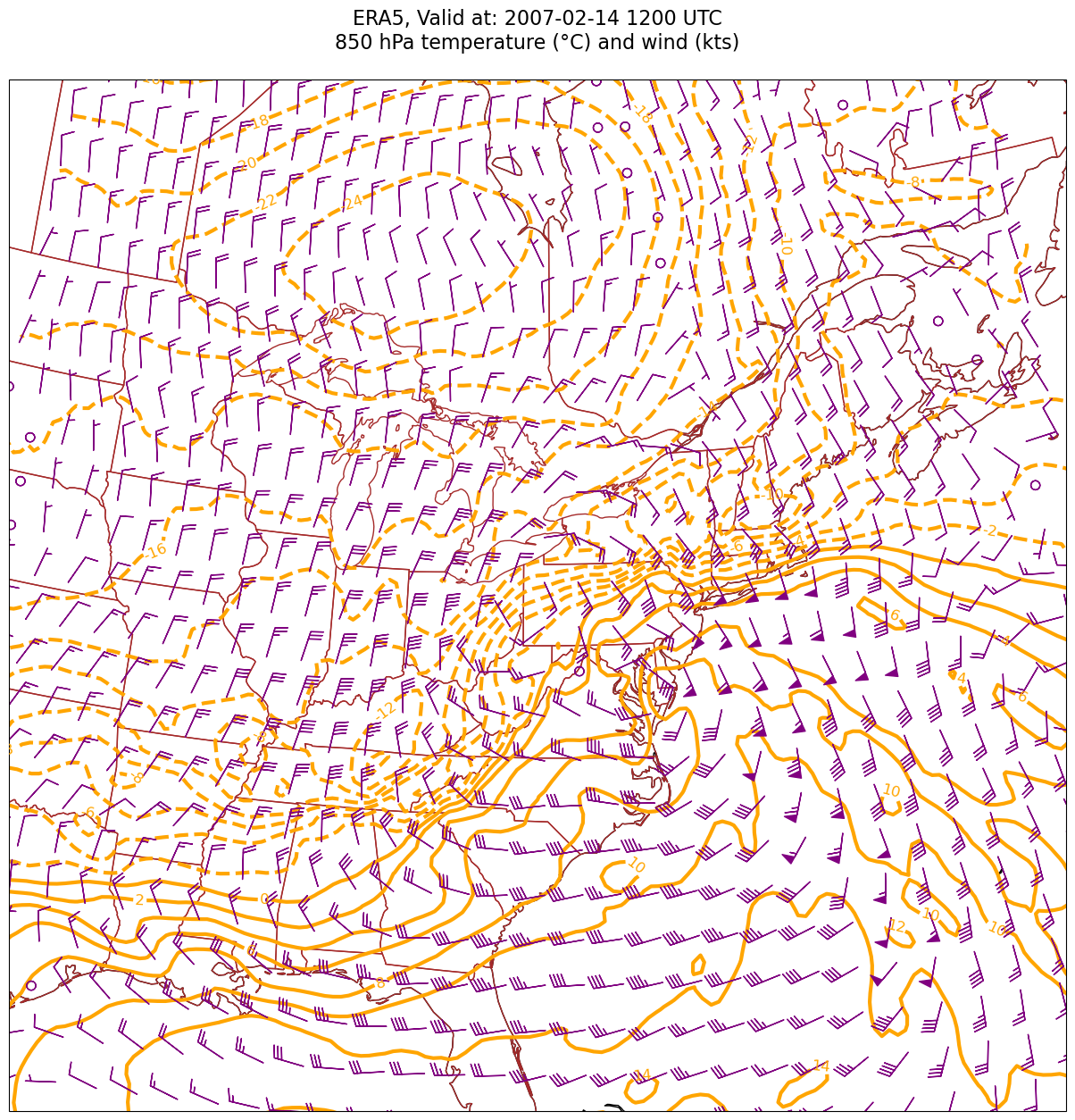
../../_images/0a6b79103e6130f19331bf3b075b27535416bfca6beac50a971f99516d8abc66.png

Look at the map and you should easily be able to identify the areas of prominent warm and cold advection. Instead of qualitatively assessing a diagnostic quantity such as temperature advection, how about we quantify it? For that, we will use MetPy’s diagnostic library, which we have imported as `mpcalc`.#

MetPy Diagnostics #

Let’s explore the `advection` diagnostic: https://unidata.github.io/MetPy/latest/api/generated/metpy.calc.advection.html #

In order to calculate horizontal tempareture advection, we need a scalar quantity (temperature, the “thing” being advected), and a vector field (wind, the “thing” doing the advecting).#

For MetPy’s advection function, we pass in the scalar, followed by the vector … in this case, T followed by U and V.

# Calculate temperature advection by the horizontal wind:
tAdv = mpcalc.advection(T, U, V)

/tmp/ipykernel_1904384/3311090283.py:2: UserWarning: Vertical dimension number not found. Defaulting to (..., Z, Y, X) order.
  tAdv = mpcalc.advection(T, U, V)

Let’s look at the output DataArray, containing the calculated values (and units) of temperature advection. Note how these values scale … on the order of 10**-5.

tAdv

<xarray.DataArray (time: 1, latitude: 128, longitude: 168)> Size: 172kB
<Quantity([[[-5.90841038e-05  6.75035204e-05  2.15284048e-05 ...  4.88857660e-06
    1.48264507e-04  2.86365599e-04]
  [-1.45538695e-05  7.32721666e-05 -9.98858574e-06 ...  2.49220104e-06
    8.21615842e-05  1.86013694e-04]
  [ 1.17928808e-04  2.44765274e-05 -8.07762443e-07 ...  4.90848057e-05
    6.14416924e-05  1.00443992e-04]
  ...
  [ 1.29052195e-05  2.14819736e-05  2.91235172e-05 ...  7.23325716e-05
    4.94348310e-05  1.14040359e-05]
  [ 1.59447393e-05  2.03775702e-05  2.48934831e-05 ...  1.00987680e-04
    7.26497877e-05  2.91857943e-05]
  [ 1.89397619e-05  2.24919900e-05  2.43124855e-05 ...  1.20025998e-04
    9.36388540e-05  4.84514254e-05]]], 'kelvin / second')>
Coordinates:
  * latitude   (latitude) float32 512B 24.0 24.25 24.5 ... 55.25 55.5 55.75
    level      int64 8B 850
  * longitude  (longitude) float32 672B 259.0 259.2 259.5 ... 300.2 300.5 300.8
  * time       (time) datetime64[ns] 8B 2007-02-14T12:00:00

Let’s get a quick visualization, using Xarray’s built-in interface to Matplotlib.

tAdv.plot(figsize=(15,10),cmap='coolwarm')

<matplotlib.collections.QuadMesh at 0x1484674790d0>

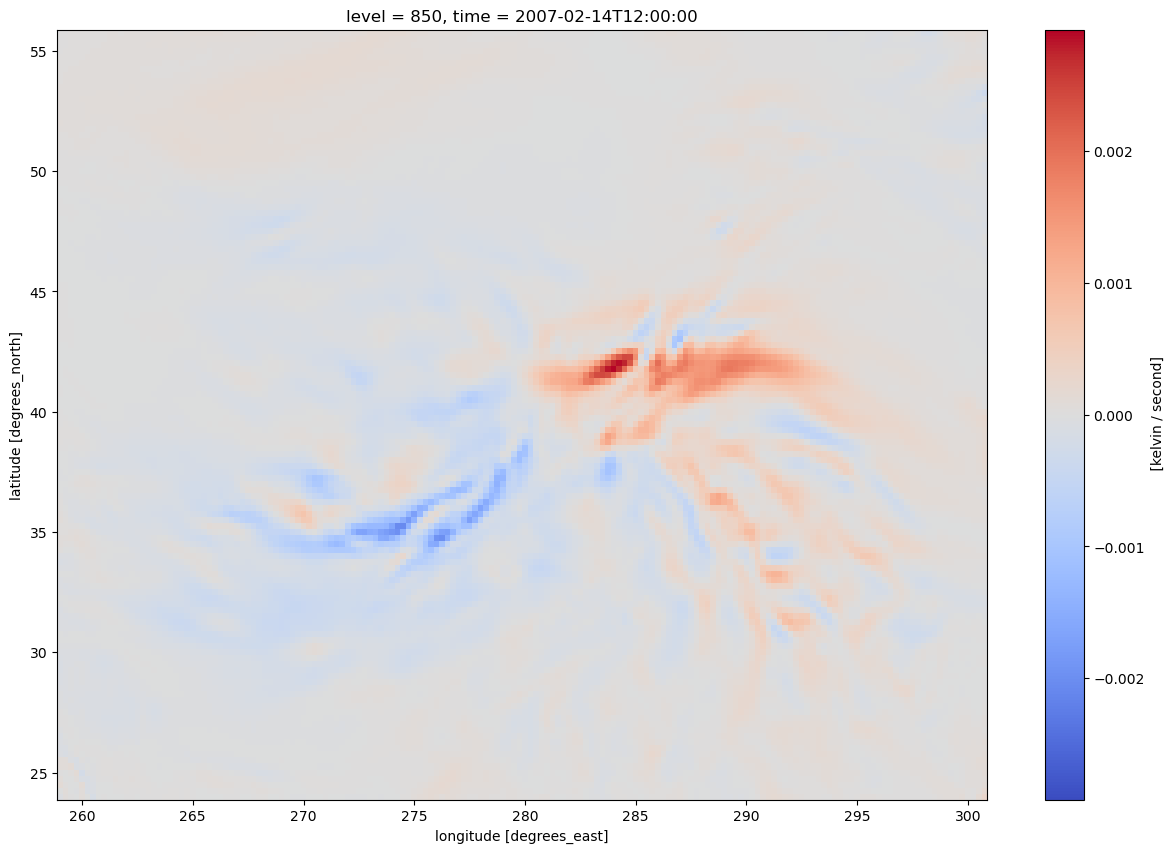
../../_images/043352d5e4f2835ca6029f34e124292357fd02c3b514319f40001bf97b64e2a1.png

We have three strategies to make the resulting map look nicer:#

Scale up the values by an appropriate power of ten
Focus on the more extreme values of temperature advection: thus, do not contour values that are close to zero.
Smooth the values of temperature advection … especially important in datasets with a high degree of horizontal resolution.

Let’s take care of the first two strategies, and then assess the need for smoothing.

Scale these values up by 1e5 (or 1 * 10**5, or 100,000) and find the min/max values. Use these to inform the setting of the contour fill intervals.#

scale = 1e5
minTAdv = (tAdv*scale).min().values
maxTAdv = (tAdv*scale).max().values
print (minTAdv, maxTAdv)

-207.64241092259962 292.19157853434

Usually, we wish to avoid plotting the “zero” contour line for diagnostic quantities such as divergence, advection, and frontogenesis. Thus, create two lists of values … one for negative and one for positive.#

advInc = 50
negAdvContours = np.arange (-300, 0, advInc)
posAdvContours = np.arange (50, 350, advInc)

negAdvContours

array([-300, -250, -200, -150, -100,  -50])

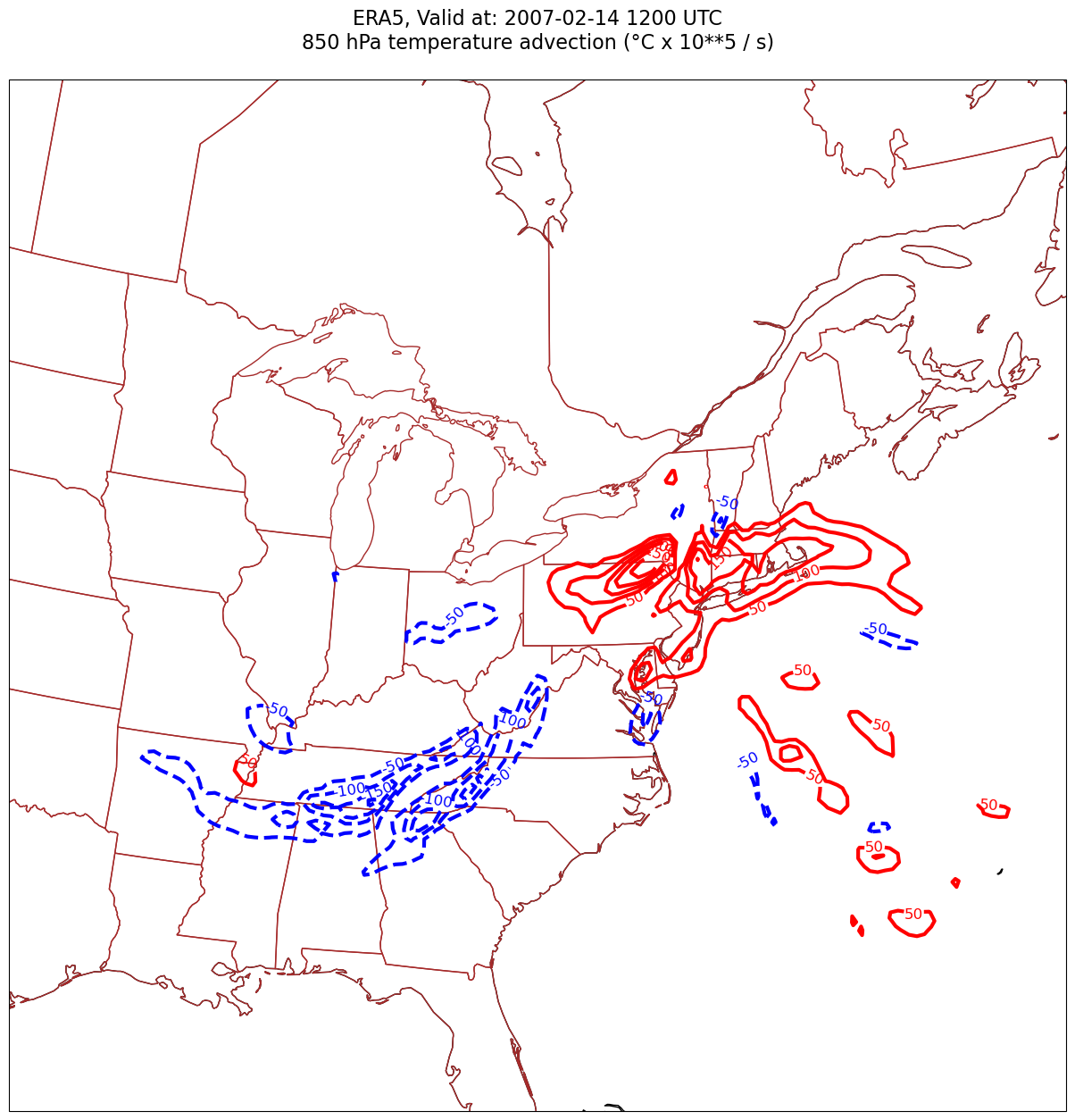
Now, let’s plot temperature advection on the map.#

for time in dateList:
    print(f'Processing {time}')
    
    # Create the time strings, for the figure title as well as for the file name.
    timeStr = dt.strftime(time,format="%Y-%m-%d %H%M UTC")
    timeStrFile = dt.strftime(time,format="%Y%m%d%H")
    
    tl1 = f'ERA5, Valid at: {timeStr}'
    tl2 = f'{levStr} hPa temperature advection (°C x 10**5 / s)'
    
    title_line = f'{tl1}\n{tl2}\n'
    
    fig = plt.figure(figsize=(21,15)) # Increase size to adjust for the constrained lats/lons
    ax = fig.add_subplot(1,1,1,projection=proj_map)
    ax.set_extent ([lonW+constrainLon,lonE-constrainLon,latS+constrainLat,latN-constrainLat])
    ax.add_feature(cfeature.COASTLINE.with_scale(res))
    ax.add_feature(cfeature.STATES.with_scale(res),edgecolor='brown')
    
    # Need to use Xarray's sel method here to specify the current time for any DataArray you are plotting.
    
    # 1a. Contour lines of warm (positive temperature) advection.
    # Don't forget to multiply by the scaling factor!
    cPosTAdv = ax.contour(lons, lats, tAdv.sel(time=time)*scale, levels=posAdvContours, colors='red', linewidths=3, transform=proj_data)
    ax.clabel(cPosTAdv, inline=1, fontsize=12, fmt='%.0f')
    
    # 1b. Contour lines of cold (negative temperature) advection
    cNegTAdv = ax.contour(lons, lats, tAdv.sel(time=time)*scale, levels=negAdvContours, colors='blue', linewidths=3, transform=proj_data)
    ax.clabel(cNegTAdv, inline=1, fontsize=12, fmt='%.0f')
    
    title = ax.set_title(title_line,fontsize=16)
    #Generate a string for the file name and save the graphic to your current directory.
    fileName = f'{timeStrFile}_ERA5_{levStr}_TAdv.png'
    fig.savefig(fileName)

Processing 2007-02-14 12:00:00

../../_images/0d219e4f771783e86178a5a7d0b410a97e69203c7249201343645a152eed30d9.png

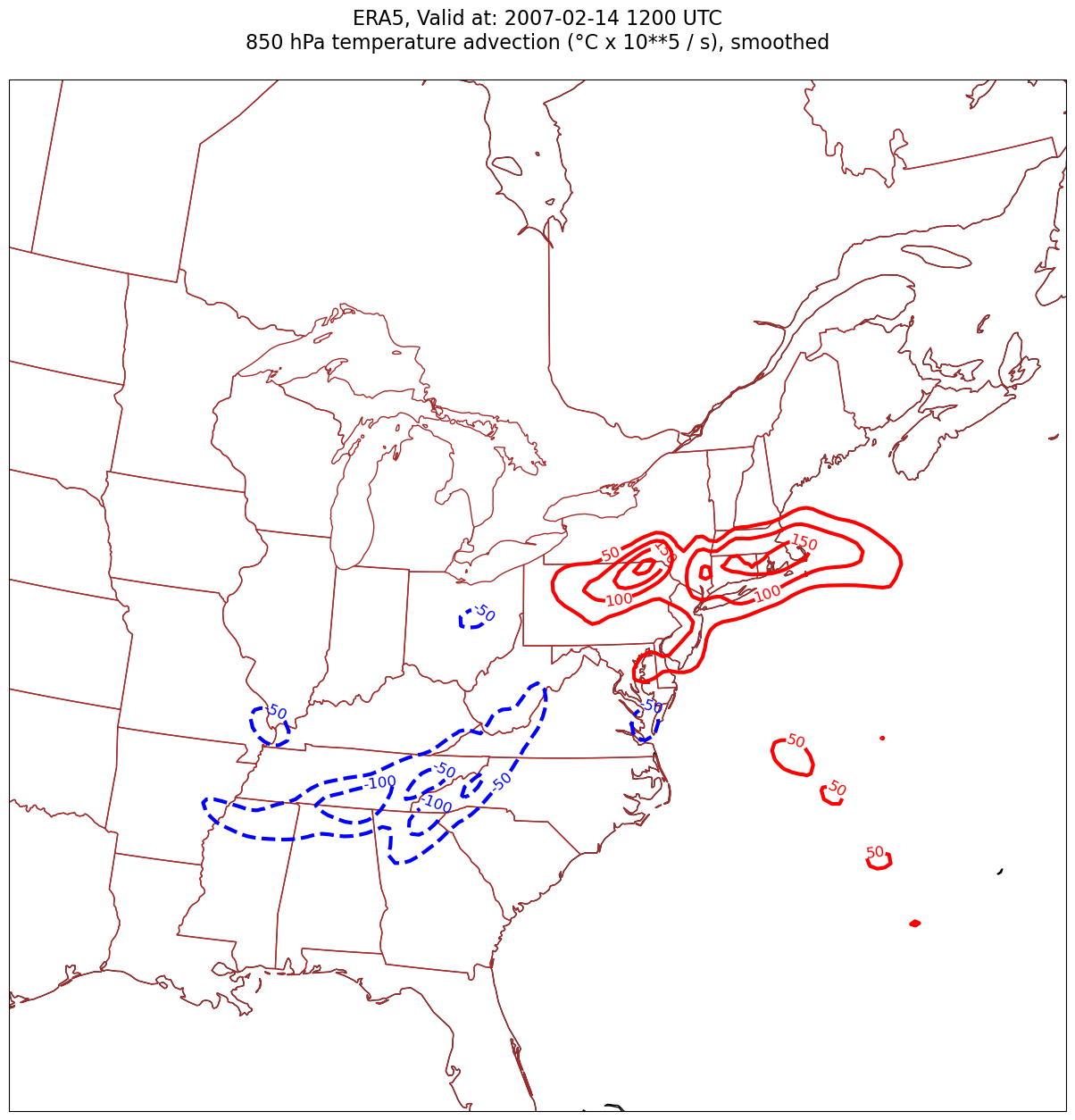
4. Smooth the diagnostic field.#

This is not a terribly “noisy” field. But let’s demonstrate the technique of employing a smoothing function. We will use a Gaussian filter, from the SciPy library, which, along with NumPy and Pandas, is one of the core packages in Python’s scientific software ecosystem.

MetPy now includes the Gaussian smoother as one of its diagnostics.

sigma = 8.0 # this depends on how noisy your data is, adjust as necessary

tAdvSmooth = mpcalc.smooth_gaussian(tAdv, sigma)

As we did before with the unsmoothed values, let’s look at the resulting DataArray and its extrema.

tAdvSmooth

<xarray.DataArray (time: 1, latitude: 128, longitude: 168)> Size: 172kB
<Quantity([[[9.05261351e-06 1.60000128e-05 1.79209784e-05 ... 7.53740688e-05
   1.20270571e-04 1.63703423e-04]
  [2.29625802e-05 2.16542267e-05 1.63649801e-05 ... 6.77532192e-05
   1.02764289e-04 1.36195195e-04]
  [3.72744157e-05 2.74612038e-05 1.46994078e-05 ... 6.04258915e-05
   8.38327163e-05 1.04600602e-04]
  ...
  [2.09302990e-05 2.39909397e-05 2.81852403e-05 ... 6.38383110e-05
   5.44033251e-05 4.35696291e-05]
  [1.98121790e-05 2.23672328e-05 2.60433055e-05 ... 7.64165278e-05
   6.49128470e-05 5.20312871e-05]
  [1.98976325e-05 2.19749433e-05 2.50980758e-05 ... 8.65473978e-05
   7.42143618e-05 6.04830767e-05]]], 'kelvin / second')>
Coordinates:
  * latitude   (latitude) float32 512B 24.0 24.25 24.5 ... 55.25 55.5 55.75
    level      int64 8B 850
  * longitude  (longitude) float32 672B 259.0 259.2 259.5 ... 300.2 300.5 300.8
  * time       (time) datetime64[ns] 8B 2007-02-14T12:00:00

scale = 1e5
minTAdv = (tAdvSmooth * scale).min().values
maxTAdv = (tAdvSmooth * scale).max().values
print (minTAdv, maxTAdv)

-143.60728535334476 209.43326543127273

Not surprisingly, the magnitude of the extrema decreased.

Plot the smoothed advection field.

for time in dateList:
    print(f'Processing {time}')
    
    # Create the time strings, for the figure title as well as for the file name.
    timeStr = dt.strftime(time,format="%Y-%m-%d %H%M UTC")
    timeStrFile = dt.strftime(time,format="%Y%m%d%H")
    
    tl1 = f'ERA5, Valid at: {timeStr}'
    tl2 = f'{levStr} hPa temperature advection (°C x 10**5 / s), smoothed'

    title_line = f'{tl1}\n{tl2}\n'
    
    fig = plt.figure(figsize=(21,15)) # Increase size to adjust for the constrained lats/lons
    ax = fig.add_subplot(1,1,1,projection=proj_map)
    ax.set_extent ([lonW+constrainLon,lonE-constrainLon,latS+constrainLat,latN-constrainLat])
    ax.add_feature(cfeature.COASTLINE.with_scale(res))
    ax.add_feature(cfeature.STATES.with_scale(res),edgecolor='brown')
    
    # Need to use Xarray's sel method here to specify the current time for any DataArray you are plotting.
    
    # 1a. Contour lines of warm (positive temperature) advection.
    # Don't forget to multiply by the scaling factor!
    cPosTAdv = ax.contour(lons, lats, tAdvSmooth.sel(time=time)*scale, levels=posAdvContours, colors='red', linewidths=3, transform=proj_data)
    ax.clabel(cPosTAdv, inline=1, fontsize=12, fmt='%.0f')
    
    # 1b. Contour lines of cold (negative temperature) advection
    cNegTAdv = ax.contour(lons, lats, tAdvSmooth.sel(time=time)*scale, levels=negAdvContours, colors='blue', linewidths=3, transform=proj_data)
    ax.clabel(cNegTAdv, inline=1, fontsize=12, fmt='%.0f')
    
    title = ax.set_title(title_line,fontsize=16)
    #Generate a string for the file name and save the graphic to your current directory.
    fileName = f'{timeStrFile}_ERA5_{levStr}_TAdvSmth.png'
    fig.savefig(fileName)

Processing 2007-02-14 12:00:00

../../_images/a269111a124f396c7f2a3a21ac5d6121928bf0fa63227a848e9f40ab8749d715.png

01_GriddedDiagnostics_TempAdvection_ERA5

Contents

01_GriddedDiagnostics_TempAdvection_ERA5#

In this notebook, we’ll cover the following:#

0) Imports #

1) Specify a starting and ending date/time, regional extent, vertical levels, and access the ERA5#

2) Specify a date/time range, and subset the desired `Dataset`s along their dimensions.#

Now create objects for our desired DataArrays based on the coordinates we have subsetted.#

3) Calculate and visualize diagnostic quantities.#

First, let’s just plot contour lines of temperature and wind barbs.#

Unit conversions#

Make the map#

MetPy Diagnostics #

Let’s explore the `advection` diagnostic: https://unidata.github.io/MetPy/latest/api/generated/metpy.calc.advection.html #

In order to calculate horizontal tempareture advection, we need a scalar quantity (temperature, the “thing” being advected), and a vector field (wind, the “thing” doing the advecting).#

We have three strategies to make the resulting map look nicer:#

Scale these values up by 1e5 (or 1 * 10**5, or 100,000) and find the min/max values. Use these to inform the setting of the contour fill intervals.#

Usually, we wish to avoid plotting the “zero” contour line for diagnostic quantities such as divergence, advection, and frontogenesis. Thus, create two lists of values … one for negative and one for positive.#

Now, let’s plot temperature advection on the map.#

4. Smooth the diagnostic field.#

01_GriddedDiagnostics_TempAdvection_ERA5

Contents

01_GriddedDiagnostics_TempAdvection_ERA5#

In this notebook, we’ll cover the following:#

0) Imports #

1) Specify a starting and ending date/time, regional extent, vertical levels, and access the ERA5#

2) Specify a date/time range, and subset the desired Datasets along their dimensions.#

Now create objects for our desired DataArrays based on the coordinates we have subsetted.#

3) Calculate and visualize diagnostic quantities.#

First, let’s just plot contour lines of temperature and wind barbs.#

Unit conversions#

Make the map#

MetPy Diagnostics#

Let’s explore the advection diagnostic: https://unidata.github.io/MetPy/latest/api/generated/metpy.calc.advection.html#

In order to calculate horizontal tempareture advection, we need a scalar quantity (temperature, the “thing” being advected), and a vector field (wind, the “thing” doing the advecting).#

We have three strategies to make the resulting map look nicer:#

Scale these values up by 1e5 (or 1 * 10**5, or 100,000) and find the min/max values. Use these to inform the setting of the contour fill intervals.#

Usually, we wish to avoid plotting the “zero” contour line for diagnostic quantities such as divergence, advection, and frontogenesis. Thus, create two lists of values … one for negative and one for positive.#

Now, let’s plot temperature advection on the map.#

4. Smooth the diagnostic field.#

2) Specify a date/time range, and subset the desired `Dataset`s along their dimensions.#

MetPy Diagnostics #

Let’s explore the `advection` diagnostic: https://unidata.github.io/MetPy/latest/api/generated/metpy.calc.advection.html #